Red-Black Tree란?
레드-블랙 트리는 각 노드에 "color"라는 추가적인 비트 정보가 담긴 self-balancing 이진 탐색 트리입니다. 노드 삽입, 삭제 시에도 균형을 유지하기에 빠른 접근을 가능하게 해주는 자료구조인데요 [2].
트리가 변경될 때마다, 새로운 트리는 재-나열(re-arrange)되고 다시 색깔이 설정되어(re-painted) 색깔 특성을 회복하고 이것은 unbalanced 트리가 worst-case가 되는 것을 막습니다.
재-균형(rebalance)은 완벽하진 않지만 O(log n)의 검색 시간을 보장합니다. 노드 삽입과 삭제 시에도 재-나열과 repaint를 포함해 O(log n) 안에 수행됩니다.
또한, 디스크 소비와 관련해서 "color"라는 추가적인 비트 정보는 노드 당 1비트를 소모하기에 기존 이진 탐색 트리 자료구조와 큰 차이가 없습니다.
이 글에서는 RB 트리와 관련해 아래와 같은 사항들을 알아보겠습니다:
- 특징
- 회전
- 삽입
- 삭제
RB 트리의 특징
RB 트리는 각 노드에 color라는 추가 정보를 저장하여 루트에서 리프까지 도달하는 경로에 존재하는 노드의 색을 제한합니다. 이를 통해, 그러한 경로들의 길이가 2배 이상 차이가 나지 않도록 하며, 대략적인 균형을 이루도록 합니다.
트리의 각 노드는 color, key, left, right, p라는 필드를 포함합니다. 만약 자식 또는 부모 노드가 존재하지 않으면 해당 노드의 포인터에는 NIL값이 들어가게 됩니다.
RB 트리는 아래와 같은 조건을 만족합니다:
- 각 노드는 red이거나 black임
- 루트 노드는 black
- 모든 리프 노드(NIL)는 black
- 노드가 red이면 자식들은 black임
- 각 노드에서 자손 리프로 가는 모든 경로는 같은 갯수의 black 노드를 가짐
RB 트리 코드 상에서 경계 조건을 처리할 때의 편의를 위해, 여기서 NIL을 나타내는 sentinel을 사용합니다. RB 트리 T에서 sentinel nil[T]는 트리 안의 같은 값을 가진 일반적인 노드입니다. sentinel의 color 필드는 BLACK이며 p, left, right, key와 같은 다른 필드는 임의의 값으로 설정될 수 있습니다. 아래 이미지에서 보이는 것처럼, NIL을 가르키는 모든 포인터들은 sentinel nil[T]를 가르키는 포인터로 대체될 수 있습니다.
여기서 sentinel을 사용하여 노드 x의 child NIL을 부모가 x인 일반적인 노드처럼 다룰 수 있습니다. 비록 트리 상에 각 NIL을 distinct한 노드로 더할 수도 있으나, 저장공간을 낭비하게 됩니다.

대신에 하나의 sentinel nil[T]가 모든 NIL을 나타내도록할 수 있습니다. 이 노드의 p, left, right, key 값은 비록 코드 상에서 세팅되더라도 사용되지 않습니다.

노드의 Black-height는 bh(x)로 표시되며, 해당 노드부터(해당 노드는 숫자에 미포함) leaf까지의 블랙 노드 수를 말합니다.
아래의 부명제(lemma)는 왜 RB 트리가 좋은 검색 트리인지 알려줍니다.
부명제: n개의 노드로 이뤄진 RB 트리의 높이는 최대 2 log(n+1)
어떤 노드 x가 루트인 서브트리는 최소한 2^bh(x) - 1개의 노드를 가진다는 것을 통해 증명을 시작할 수 있습니다. 이것은 x의 높이에 대한 귀납적 방식으로 증명할 수 있는데요. 만약 x의 높이가 0이라면, x는 반드시 leaf(nil[T[)이어야 하고, x가 루트인 서브트리는 최소한 2^bh(x) - 1 = 2^0 - 1 = 0 개의 노드로 구성됩니다.
귀납적 방식으로, 노드 x가 양수의 높이를 가지며 2개의 자식을 가진 내부 노드가 있다고 하겠습니다. 각 자식은 bh(x) 또는 bh(x) -1인 black-height를 가집니다. x의 자식의 높이가 x의 높이 보다는 작기 때문에, 귀납적 가설을 통해 각 자식은 최소한 2^(bh(x)-1) - 1개의 노드를 가진다는 것을 알 수 있습니다. 그러므로 x가 루트인 서브트리는 최소한 (2^(bh(x)-1) - 1) + (2^(bh(x)-1) - 1) + 1 = 2^bh(x) - 1개의 노드를 가집니다.
부명제를 완성하기 위해, h가 트리의 높이라고 하겠습니다. RB 트리 특징의 4번을 통해서 어떤 한 개의 루트에서 leaf로의 path는 언제나 루트 제외 최소한 반 이상의 노드가 검은색임을 알 수 있습니다. 결과적으로 루트의 black-height는 최소한 h/2보다 큽니다.
그러므로, n >= 2^(h/2) - 1입니다.
정리하면, h <= 2 log(n+1)이 됩니다.
이 부명제의 직접적인 결과는 Search, Minimum, Maximum, Successor, Predecessor과 같은 동적 set 연산이 O(lg n)에 구현될 수 있다는 점입니다. 그 이유는 그러한 연산들은 검색 트리 높이가 h인 트리에 대해 O(h)안에 수행되며 n 노드로 구성된 RB 트리는 높이가 O(lg n)인 검색트리이기 때문입니다.
일반 트리에서 insert, delete가 O(lg n)이나 RB 트리에서는 그러한 연산 이후 변형된 이진 검색 트리는 RB 트리가 아니기 때문에 RB 트리에는 해당되지 않습니다.
회전
insert, delete와 같은 검색 트리 연산이 n개 노드의 RB 트리에서 수행될 때에는 O(lg n) 시간이 걸립니다. 2가지 연산은 트리를 변형하기 때문에, 연산 직후의 트리를 RB 트리의 특징을 위반합니다. RB 트리의 특징을 다시 회복하기 위해서, 연산 직후의 변형된 트리에 대하여 노드의 색을 변경하거나 포인터 구조를 재조정해주어야 합니다.
포인터 구조 재조정은 회전을 통해서 수행합니다. 이 회전은 이진 검색 트리의 특징을 보존하는 검색 트리에서의 로컬 연산인데요. left와 right 2가지 회전이 존재합니다. 노드 x에 대하 좌-회전을 수행할 때에는 x의 오른쪽 자식인 y가 nil[T]이 아니여야 합니다. 좌-회적은 x에서 y로의 링크전달을 통해 '피봇'하는데요. 이것은 y가 서브트리의 새로운 루트가 되게하며 x는 y의 왼쪽 자식이, y의 왼쪽 자식이었던 것은 x의 오른쪽 자식이 되게 합니다.

Left-Rotate(T, x)의 로직은 아래와 같습니다:
y <- right[x]
right[x] <- left[y]
if left[y] != nil[T]
then p[left[y]] <- x
p[y] <- p[x]
if p[x] == nil[T]
then root[T] <- y
else if x == left[p[x]]
then left[p[x]] <- y
else right[p[x]] <- y
left[y] <- x
p[x] <- y좌-회전 및 우-회전 모드 O(1)으로 동작합니다. 회전으로 포인터만 변경되며, 다른 필드들은 똑같습니다.
삽입
n 노드인 RB 트리에 하나의 노드를 삽입하는 것은 O(lg n)으로 동작합니다. 일반 트리에서의 삽입에서 조금 변형된 형태로 수행하게 되는데요. 일반 트리에서의 insert와 같이 하나의 노드를 트리 T에 삽입하고 삽입한 노드의 색을 red로 표시합니다. RB 트리의 특징이 보존되기 위해서, 추가적인 프로시져인 RB-Insert-Fixup을 호출하여 어긋난 노드들의 색을 다시 칠하고 회전도 수행합니다. RB-Insert(T, z)는 노드 z를 RB 트리 T에 삽입합니다.
y <- nil[T]
x <- root[T]
while x != nil[T]
do y <- x
if key[z] < key[x]
then x <- left[x]
else x <- right[x]
p[z] <- y
if y == nil[T]
then root[T] <- z
else if key[z] < key[y]
then left[y] <- z
else right[y] <- z
left[z] <- nil[T]
right[z] <- nil[T]
color[z] <- RED
RB-Insert-Fixup(T, z)
RB-Insert-Fixup은 아래와 같습니다:
while color[p[z]] == RED
do if p[z] == left[p[p[z]]]
then y <- right[p[p[z]]]
if color[y] == RED
then color[p[z]] <- BLACK # case 1
color[y] <- BLACK
color[p[p[z]]] <- RED
z <- p[p[z]]
else if z == right[p[z]] # case 2
then z <- p[z]
Left-Rotate(T, z)
color[p[z]] <- BLACK # case 3
color[p[p[z]]] <- RED
Right-Rotate(T, p[p[z]])
else (same as then clause with "right" and "left" exchanged)
color[root[T]] <- BLACK
RB-Insert-Fixup을 이해하기 위해서, 3가지 단계로 나눠서 이해해보겠습니다.
먼저, 노드 z가 삽입되고 red로 칠해졌을 때 RB 트리의 어떤 특징이 위반되었는지 알아봅니다. 두 번째로 위 코드의 while 루프를 살펴보겠습니다. 마지막으로 코드 상의 3가지 케이스로 나누어 각각 어떤 방식으로 목적을 달성하는지 살펴보겠습니다.
RB-Insert-Fixup 이후에는 RB 트리의 어떤 특징이 위반될까요?
다시 한 번 RB 트리의 특징을 살펴보면 아래와 같습니다:
- 각 노드는 red이거나 black임
- 루트 노드는 black
- 모든 리프 노드(NIL)는 black
- 노드가 red이면 자식들은 black임
- 각 노드에서 자손 리프로 가는 모든 경로는 같은 갯수의 black 노드를 가짐
새로이 삽입되는 red 노드의 자식들을 모두 sentinel nil[T]이기 때문에 1, 3은 그대로 유지됩니다. 특징 5 또한 삽입되는 노드 z는 sentinel(black)을 대체하며 z 자신은 red, sentinel인 2 자식은 black이기에 유지됩니다. 그러므로 위한되는 특징은 2, 4가 해당됩니다.
z가 red이기에 2가지 모두 위반이 가능한데요. 특징 2는 z가 루트라면 위반되고, 특징 4는 z의 부모가 red라면 위반됩니다.
아래 이미지는 그렇게 위반된 상태가 위 코드의 while 루프를 통해 3가지 케이스로 처리되는 과정을 보여줍니다:
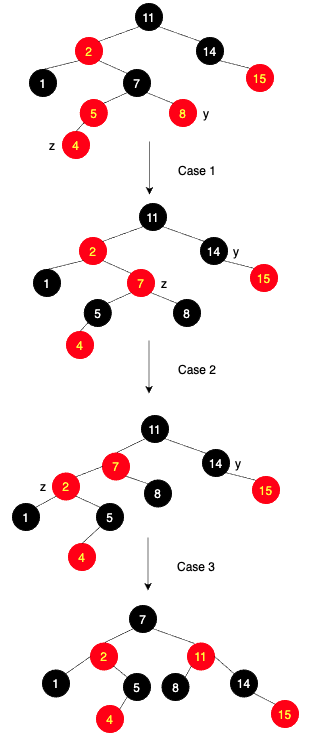
루프의 시작 전에
- 노드 z는 red
- p[z]가 루트라면, p[z]는 black
- RB 트리 특징을 위반한다면, 최대 1개의 위반사항이 있고 그것은 특징 2이거나 4임. 특징 2를 위반했다면, z가 루트이고 red라서 그렇고 4를 위한했다면 z와 p[z] 둘다 red라서 위반함.
위 이미지에서는 맨 특징 4를 위반한 사례를 보여주고 있습니다.
그 흐름을 좀 더 상세하게 살펴보면,
초기화
루프의 첫 순회 전에, 위반사항이 없는 RB 트리에 red 노드인 z를 추가했습니다. RB-Insert-Fixup이 호출될 때에는 아래와 같은 상황입니다:
- RB-Insert-Fixup이 호출될 때, z는 추가된 red 노드임
- p[z]가 루트라면, p[z]는 black으로 시작했고 RB-Insert-Fixup이 호출되기 전에 변경되지 않았음
- RB-Insert-Fixup이 호출될 때 특징 1, 3, 5는 유지됨. 특징 2 위반 시에는 red 노드는 새롭게 추가된 노드 z이며 트리 상의 유일한 노드임. z의 자식들은 모두 sentinel이므로 위반은 오직 해당 노드 색이 red인데서 기인함. 특징 4 위반 시에는 z의 자식들은 sentinel이므로 z와 p[z]가 red라서 발생하게 됨.
종료
루프가 종료되면, p[z]가 black이라서 종료하게 됩니다. 그러므로 특징 4에 대한 위반은 루프 종료 시 사라지게 됩니다. 루프 수행 이후 남을 수 있는 위반은 그렇기에 특징 4인데, 이 부분로 16번째 줄의 수행을 통해서 사라지며 RB-Insert-Fixup 수행 이후에는 모든 RB 트리 특징을 만족하게 됩니다.
유지
while 루프 상에서는 실제로 6개의 케이스로 갈라지게 되나, 3개는 다른 3개와 정확히 반대이며 오직 z의 부모인 p[z]가 z의 조부모의 좌측인지 우측인지에 따라 차이가 존재합니다. p[p[z]]는 p[z]가 루트라면 존재하지 않는데, 오직 루프는 p[z]가 red일때만 실행되고 red라면 루트일 수 없기 때문에(특징 2) 루프가 실행되었다면 p[p[z]]는 언제나 존재합니다.
Case 1은 case 2와 3과 달리 z의 부모의 형제(uncle)의 색이 red입니다. 코드 3번째 줄에서 right[p[p[z]]]를 통해 uncle에 접근하여 색을 체크합니다.
Case 1: z의 uncle이 red일 때
Case 1은 p[z]와 y 모두 red일 때 실행됩니다. p[p[z]]는 black이기 때문에, p[z]와 y 모두 black으로 칠할 수 있는데요. z와 p[z]가 모두 red인 문제를 해결하고 p[p[z]]를 red로 변경하여 특징 5를 유지할 수 있습니다. 이후 while 루프를 p[p[z]]를 새로운 노드 z로 만들어 반복할 수 있습니다. 포인터 z는 트리 상에서 2레벨 위로 올라가게 됩니다.
z는 현재 순회에서의 노드 z를 나타내고 z' = p[p[z]]는 다음 순회에서의 z를 나타냅니다.
- 이 순회는 p[p[z]]를 red로 만들기에, z'는 다음 순회의 z가 됩니다.
- 노트 p[z']는 이번 순회의 p[p[p[z]]]이기에, 이 노드의 색은 변경되지 않습니다. 이 노드가 루트라면, 이번 순회 전에 black이고 다음 순회 시작점에서도 black이게 됩니다.
- case 1은 특징 5를 유지하기에, 특징 1, 3을 위반하지 않습니다. 만약 z'가 다음 순회에서 루트라면, case 1은 유일한 위반인 특징 4를 해당 순회에서 교정하게 됩니다. z'가 red이고 루트이기 때문에, 특징 2는 위반되는 유일한 사항이 됩니다. z'가 다음 순회에서 루트가 아니라면, case 1은 특징 2를 위반하지 않습니다. case 1은 유일한 위반인 특징 4를 교정하게 되는데요. z'를 red로 만들어 p[z']만 남겨둔 후, p[z']가 black이면 특징 4를 위반하지 않게 됩니다. p[z']가 red면, z'를 red로 변경하는 것은 특징 4를 위반하고 다음 루프로 넘어가게 됩니다.
Case 2, 3: z'의 uncle y가 black이고 z가 오른쪽 자식일 때, z'의 uncle y가 black이고 z가 왼쪽 자식일 때
Case 2, 3의 경우에는, z의 uncle y는 black입니다. 2 케이스는 z가 p[z]의 오른쪽 자식인지 왼쪽 자식인지에 따라 구분되는데요.
Case 2의 경우에 z는 부모의 오른쪽 자식입니다. 그렇기에 좌-회전을 사용해 case 3으로 변경할 수 있습니다. z와 p[z] 모두 red이기 때문에, 회전은 특징 5와 노드의 black-height 어느 쪽에서 영향을 미치지 않습니다. case 3을 직접 또는 case 2 이후에 마주한 경우에, z의 uncle y는 black입니다.
코드 2, 3번째 줄이 실행됬다면 p[p[z]]는 존재하게 됩니다. 또한, 코드 상에서 z를 10 번째 줄에서 1 레벨 올렸다가 11번째 줄에서 1레벨 내린 후에 p[p[z]]는 변경되지 않고 그대로 존재합니다. case 3의 경우에, 색을 조금 변경해주고 우-회전을 진행하면 특징 5를 여전히 따르며 더 이상 한 row에 2개의 red를 가지지 않기에 종료됩니다. p[z]는 이제 black이기 때문에 while 루프는 더 이상 실행되지 않습니다.
- Case 2는 z가 red인 p[z]를 가르키도록 만듭니다. case 2, 3의 경우에 z에 어떠한 변경도 발생하지 않습니다.
- Case 3은 p[z]를 black으로 만들어, 만약 p[z]가 다음 순회에서 루트라면 black일 수 있도로 합니다.
- Case 1과 같이 특징 1, 3, 5는 case 2, 3에서 유지됩니다. 노드 z는 case 2, 3의 경우에 루트가 아니기에, 특징 2를 위반하지 않는 다는 사실을 알 수 있습니다. Case 2, 3은 특징 2의 위반을 만들지도 않는데, case 3의 회전에 의해서 유일한 red 노드는 black 노드의 자식이 되기 때문입니다.
위와 같이 루프의 매 순회가 변하지 않음을 보임으로써, RB-Insert-Fixup이 정확하게 RB 트리의 특징을 회복하는 것을 알 수 있습니다.
분석
RB-Insert의 수행 시간은 n 개의 노드로 이뤄진 RB 트리의 높이는 O(lg n)이고, 코드의 수행은 O(lg n)입니다. RB-Insert-Fixup은 오직 case1이 수행될 때만 반복되며 포인터 z는 2레벨씩 트리를 올라갑니다. 그렇기에 while 루프가 실행되는 총 횟수는 O(lg n)입니다. 그러므로, RB-Insert는 총 O(lg n)에 수행됩니다.
삭제
n개의 노드로 이뤄진 RB 트리의 다른 기본 연산과 같이, 노드의 삭제는 O(lg n)에 수행됩니다. RB 트리에서 노드를 삭제하는 것은 삽입하는 것보다 약간 더 복잡한데요.
노드를 제거한 이후에, 보조적인 RB-Delete-Fixup을 호출하여 RB 트리 특징 회복을 위해 회전과 색변경을 수행합니다.
if left[z] == nil[T] or right[z] == nil[T]
then y <- z
else y<- Tree-Successor(z)
if left[y] != nil[T]
then x <- left[y]
else x <- right[y]
p[x] <- p[y]
if p[y] == nil[T]
then root[T] <- x
else if y == left[p[y]]
then left[p[y]] <- x
else right[p[y]] <- x
if y != z
then key[z] <- key[y]
copy y satellite data into z
if color[y] == BLACK
then RB-Delete-Fixup(T, x)
return y
RB-Delete-Fixup에 전달되는 x는 다음 2가지 중에 하나입니다. 첫 번째는 y가 떨어나가기 전에 y가 sentinel nil[T]가 아닌 유일한 자식을 가지고 있으면 그 유일한 자식이 x가 됩니다. 두 번째는 y가 자식이 없고, x가 sentinel nil[T]이 될 수 있습니다. 후자의 경우에, 7번째 줄에서 x의 부모가 이전에 y의 부모였던 노드가 되도록 합니다.
RB-Delete-Fixup은 아래와 같습니다:
while x!= root[T] and color[x] == BLACK
do if x == left[p[x]]
then w <- right[p[x]]
if color[w] == RED
then color[w] <- BLACK # case 1
color[p[x]] <- RED
Left-Rotate(T, p[x])
w <- right[p[x]]
if color[left[w]] == BLACK and color[right[w]] == BLACK
then color[w] <- RED # case 2
x <- p[x]
else if color[right[w]] == BLACK
then color[left[w]] <- BLACK # case 3
color[w] <- RED
Right-Rotate(T, w)
w <- right[p[x]]
color[w] <- color[p[x]] # case 4
color[p[x]] <- BLACK
color[right[w]] <- BLACK
Left-Rotate(T, p[x])
x <- root[T]
else (same as then clause with "right" and "left" exchanged)
color[x] <- BLACK
만약 떨어져 나가는 노드 y가 black이라면, 3가지 문제가 발생합니다. 첫 번째는, y가 루트이었고 y의 red 자식이 새로운 루트 노드가 된다면 특징 2를 위반합니다. 두 번째로, x와 p[y]가 red라면, 특징 4를 위반합니다. 세 번째로, y의 삭제는 y를 포함했던 모든 path가 1개 적은 black 노드를 가지도록 합니다. 그러므로, 특징 5를 위반하게 됩니다. 이 문제는 노드 x가 추가적인 black을 가지도록 만들면서 해결할 수 있는데요. 자식이 black을 1개 더 가진다고 가정하고, 일단 black 노드 y를 도려내면서 자식에서 black을 푸시할 수 있습니다. 이제 문제는 x가 red도 아니고 black도 아니어서 특징 1을 위반하게 됩니다. 노드 x는 이전의 가정으로 인해 "doubly black"이거나 "red이고 black"인 상태가 되는데요. x의 color attribute는 RED이거나 BLACK이어야 하기에, 추가적인 black은 color attribute 대신 x의 포인팅에 반영되어야 합니다.
그렇기에 RB-Delete-Fixup의 while 루프의 목적은 추가적인 black을 트리 위로 아래의 조건을 만족할 때까지 올리는 데 있습니다:
- x가 red이고 black인 노드를 가르키면, x를 black 처리하고,
- x가 루트를 가르키면 추가적인 black은 간단히 제거되거나,
- 적절한 회전이나 색 변경이 수행될 때까지
while 루프 안에서, x는 언제나 루트가 아닌 doubly black 노드를 가르킵니다. 포인터 w는 x의 형제(sibling)를 가르키도록 합니다. 노드 x가 doubly black이기 때문에, 노드 w는 nil[T]될 수 없는데요. w가 nil[T]이라면 p[x]에서부터 leaf w까지의 black-height는 p[x] - x보다 작을 것이기 때문입니다.
4가지 케이스는 아래 이미지와 같습니다:
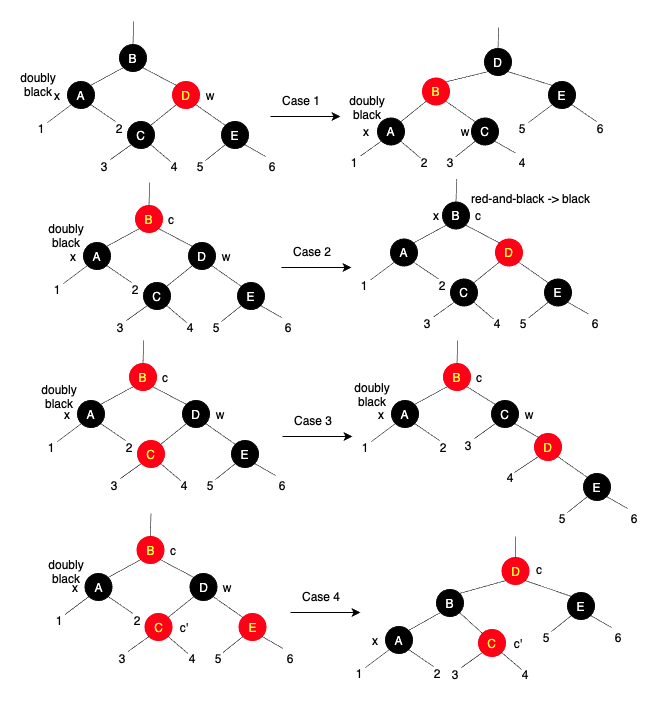
각 케이스를 살펴보기 전에, 일반적으로 어떻게 특징 5를 유지하는지 알아보면 서브트리에서의 black-height를 유지하는 것이 핵심 로직입니다. 그러므로, 이전 단계의 변형에서 특징 5가 유지된다면, 이후에도 계속 유지되게 됩니다.
Case 1: x의 형제 w가 red인 경우
case 1은 x의 형제인 w가 red일 때 발생합니다. w는 black 자식들을 가져야만 하기에, w와 p[x]의 색을 변경하고 p[x]에 좌-회전을 수행하며 RB 트리 특징을 모두 유지할 수 있습니다. x의 새로운 형제는 회전 전의 w의 자식들 중 하나인데 이제 black이기에 case 2, 3, 4로 넘어가게 됩니다. case 2, 3, 4는 노드 w가 black일 때 발생하고 w의 자식들의 색으로 구분됩니다.
Case 2: x의 형제 w가 black이고 w의 자식 모두가 black인 경우
case 2에서 w 자식 2개 모두는 black입니다. w도 black이기에, x와 w에서 모두 black을 하나씩 제거하여 x는 single black이 되고, w는 red가 됩니다. x와 w에서 black을 제거하는 것을 상쇄하기 위해서 (이전에 black이거나 red였을 수 있는) p[x]에 추가적인 black을 더합니다.
이러한 과정을 p[x]가 새로운 x가 되며 while 루프에서 반복하게 됩니다. case 2를 case 1을 통해서 마주하고, 원래 p[x]는 red 였기에 새로운 노드 x는 red-and-black이 됩니다. 그러므로 새로운 노드 x의 color attribute 값 c는 RED이고 루프는 루프 조건을 체크하며 종료되고, 새로운 노드 x는 singly black으로 마지막 줄에서 처리됩니다.
Case 3: x의 형제 w가 black이고, w의 좌측 자식이 red이며, 우측 자식은 black일 때
case 3은 w가 black, w의 좌측 자식이 red, 우측 자식이 black일 때에 발생합니다. w와 left[w]의 색을 변경하고 w에 대해 우-회전을 수행하면서 특징을 유지할 수 있는데요. x의 새로운 형제 w는 black이고 새로운 형제 w의 우측 자식은 red이므로 case 4로 넘어가게 됩니다.
Case 4: x의 형제 w가 black이고, 우측 자식은 red일 때
case 4는 x의 형제 w가 black이고, 우측 자식은 red일 때 발생합니다. 몇가지 색 변경을 수행하고 p[x]에 대해 좌-회전을 수행하여 x에 있는 추가적인 black으르 제거하고 singly black으로 만들며 특징도 유지할 수 있습니다.
이후 x에 루트를 설정하여 루프 조건을 벗어나 종료되게 됩니다.
분석
n개 노드로 이뤄진 RB 트리의 높이는 O(lg n)이고, RB-Delete-Fixup은 O(lg n)에 수행됩니다. RB-Delete-Fixup 내에서 case 1, 3, 4는 constant한 횟수의 색상변경과 최대 3회의 회전 이후에 종료되게 되는데요. Case 2는 while 루프가 반복되는 유일한 케이스로 포인터 x는 트리를 최대 O(lg n)번 올라가며 수행되고 회전을 존재하지 않습니다. 그러므로 RB-Delete-Fixup은 O(lg n)와 최대 3회의 회전으로 수행되며 RB-Delete의 총 성능은 또한 O(lg n)이게 됩니다.
Reference